| « Snow Crystal Variety and the Bentley Length Scale in Clouds | The Jericho Farmer and the Electric Crystals » |
Parting and Bending of Hair Ice
Hair ice often shows a clear "parting".
By part, I refer to that line along the underlying log surface, either side of which the hair tilts further to the side, analogous to the part one makes in one's own hair with a comb. An explanation for the cause of the part is unlikely to be found in the nature of the pores (from which the ice originates), but rather in the differing rates of growth of adjacent hairs.
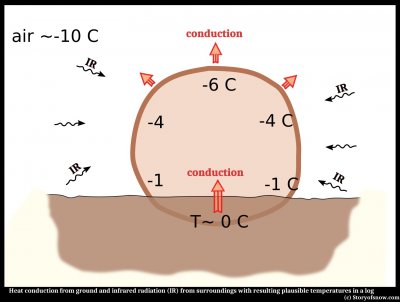
Even though we might not have a complete theory of hair-ice growth, we do know that the formation depends on temperature. And so it also must follow that the rate of growth (e.g., centimeters per hour) depends on temperature. Very close to melting, the rate must be low, and at very low temperatures the rate must decrease to zero due to the entire log freezing. In general, the lower the temperature, the faster ice grows from its melt. So, it is reasonable to assume that the rate of growth of each hair increases as the pore temperature decreases. (The following discussion assumes this to be the case, though the assumption is not required for the basic argument.) Below is an example of a plausible temperature distribution. I put in specific temperatures (in Celcius) mainly for conciseness--they are made up.
There are two main reasons that the top of a log would often be its coldest point as sketched above. One is the greater distance from the warmer ground and the second is the lower flux of infrared radiation from the surroundings to the top of the log. And so, the coldest region should often be a line along the top, or near the top, of the log.
Of course, if one side of the log has closer trees, bushes, or rocks, then this line of coldest temperature will shift a little to the other side of the log.
Finally, why should the line of coldest temperature equal the parting line? Consider two hairs, side-by-side. At some point along the hair, maybe near the ends, the hairs may touch. With a little bit of cohesion, these points of contact may remain points of contact as the hairs grow from the base. In this case, the faster-growing hair will push on the contact point while the slower hair will pull. To remain in contact, the faster hair bends toward the slower-growing hair. As the slower-growing hair is further from the part, the other hair bends away from the part.
You can see this yourself by cutting a strip of paper. Fold the strip in half, the fold representing the fixed contact point, pinch the other end of the doubled-over strip, and slide one strip over the other. Watch as both bend.
Some cases of hair ice do not show a clear part, yet have many bent hairs. The same argument may apply, except that either the temperature differences on the log are more complex or the points of contact are more random. Many irregularities in the surroundings and log are possible. Note though that a single hair may bend by the same argument: even though the temperature change across a pore may be tiny, the two sides of the hair are very close. That is, if you think about it, the relevant quantity is not the temperature difference itself, but the temperature gradient.
--JN